前言

一般在部署检测或分割模型时，只会将模型本身转换到推理框架下，其他预处理与后处理操作是在cpu下执行，如果后处理中有较多耗时操作，会影响到整体推理速度，比如nms算法需要并行化加速，非常适合GPU执行，所以可以将nms算法使用cuda kernel实现或直接部署到推理框架下。

本文记录了将solov2包括后处理的matrix-nms都使用后一方式部署，在部署过程中的一些需要注意的地方。

正文

一、模型本身转换

solov2的模型本身部署问题不大，需要注意的算子是linspace和GN(Group Normalization)。

二、动态卷积转换

solov2中使用的动态卷积是卷积核尺寸变化的卷积，由于TensorRT不支持动态的卷积核，所以需要将卷积操作转换成矩阵操作代替，在pytorch底层其实卷积操作就是矩阵操作。

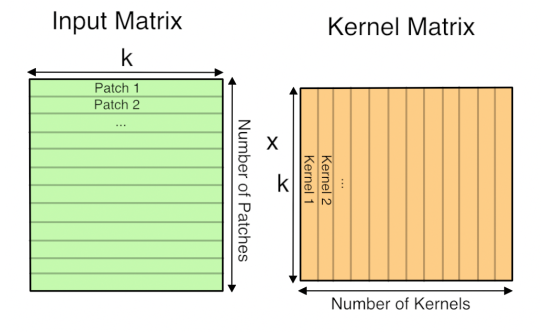
简单介绍下转换的原理，其实就是通过卷积核与输入矩阵进行卷积，把输入图像划分成若干个块，如果将若干块分别展开成一维向量，拼接成二维矩阵，再把卷积核采用同样方式进行展开，卷积就可以表示为输入图像展开的二维矩阵与卷积核展开的二维矩阵进行矩阵运算torch.matmul。


via 卷积操作转化成矩阵乘法

三、后处理部分

后处理部分主要就是为了执行NMS得到候选框，得到最终需要的mask与label，通常部署模型是不直接部署进推理引擎中，而是直接c++实现或cuda kernel实现。

NMS(Non-maximum suppression/非极大值抑制)

NMS算法一般是为了去掉模型预测后的多余框,即找到局部极大值，并筛除（抑制）邻域内其余的值。

传统NMS的缺点是不能有效应对重叠区域的不同物体的预测，比如图片上有重叠的两个类别一样的物体，用传统的nms置信度较低的那一个很可能被去除，但其实他们框的是两个不一样的物体。

于是Soft-NMS提出：不是将低于阈值的直接置为0，而是通过将其根据IoU大小来进行惩罚衰减，衰减系数降低的方式有linear和gaussian。

同时NMS由于顺序处理的原因，运算效率较为低下,极大影响了模型的效率。于是solov2算法提出Matrix-NMS，NMS的一种并行化方案，可以使用GPU并行计算，并且Matrix-NMS是针对mask IoU进行预测，会比box IoU更加耗时，因此加速非常重要。

Matrix-NMS原理

Matrix-NMS的原理可以阅读matrix-nms原理，解释的很清楚，以下贴的是matrix-nms伪代码与solov2实现的matrix-nms的pytorch源码：


via matrix-nms伪代码

    num_masks = len(labels)
    flatten_masks = masks.reshape(num_masks, -1)
    # inter.
    inter_matrix = torch.mm(flatten_masks, flatten_masks.transpose(1, 0))
    expanded_mask_area = mask_area.expand(num_masks, num_masks)
    # Upper triangle iou matrix.
    iou_matrix = torch.triu(inter_matrix /
                  (expanded_mask_area + expanded_mask_area.transpose(1, 0) -
                   inter_matrix),diagonal=1)
    # label_specific matrix.
    expanded_labels = labels.expand(num_masks, num_masks)
    # Upper triangle label matrix.
    label_matrix = torch.triu((expanded_labels - expanded_labels.transpose(
        1, 0) == 0).float(),diagonal=1)

    # IoU compensation
    compensate_iou, _ = (iou_matrix * label_matrix).max(0)
    compensate_iou = compensate_iou.expand(num_masks,
                                           num_masks).transpose(1, 0)

    # IoU decay
    decay_iou = iou_matrix * label_matrix

    # Calculate the decay_coefficient
    if kernel == 'gaussian':
        decay_matrix = torch.exp(-1 * sigma * (decay_iou**2))
        compensate_matrix = torch.exp(-1 * sigma * (compensate_iou**2))
        decay_coefficient, _ = (decay_matrix / compensate_matrix).min(0)
    elif kernel == 'linear':
        decay_matrix = (1 - decay_iou) / (1 - compensate_iou)
        decay_coefficient, _ = decay_matrix.min(0)
    else:
        raise NotImplementedError(
            f'{kernel} kernel is not supported in matrix nms!')

在转换过程中有一下几个部分需要特别注意：
输出可变索引

在筛选候选框时会将低于score_thr阈值和mask_thr阈值的筛掉，此过程使用到了nonzero算子和切片操作，输出的是一个不固定大小的序列，而在TensorRT中明确不支持输出动态的操作，因此处理方式是筛选，而是根据score大小进行排序。

由于不进行筛选操作，在计算mask区域时会出现没有mask的情况，需要注意此时作为除数时需要增加一个极小数，防止除数为0

topK输入

由于上面已经将筛选过程去掉，但是不同输入图片的候选框肯定是不同的，而TensorRT不支持输出动态，因此固定输出候选框的个数仍然有必要，此时需要手动配置一个固定的候选框个数num_pre。

在pytorch中后处理逻辑是先筛选，在计算NMS时按score排序，我们在转换到TensorRT时由于底层限制，是先排序，所以此时可以根据num_pre作筛选。

TensorRT中无法使用sort算子，因为需要固定topK的输入大小，而有了num_pre参数就可以对候选框做截断或补齐了。
float数据转换

在python下测试推理时会出现的情况，指的是pytorch的cuda类型数据在浮点运算后会改变数据类型，变为float64类型，而TensorRT推理时直接输入会溢出，导致结果出错，所以需要在cuda数据运算后再作一次强制类型转换。